1. 一个圆柱形状的量杯中放有一根长为12厘米的细搅棒(搅棒直径不计)，当搅棒的下端接触量杯下底时，上端最少可露出杯口边缘2厘米，最多可露出4厘米，那么这个量杯的容积是多少立方厘米?

　　A.65π

　　B.72π

　　C.96π

　　D.108π

　　2. 修建一条长300米的混凝土大坝，横断面为等腰梯形，上下底和腰长分别为6米、18米、10米，问共需多少方混凝土?

　　A.480

　　B.4800

　　C.19200

　　D.28800

　　3. 如果将长、宽、高为三个连续整数的长方体的各边长均增加2后，新长方体的体积将增加4倍，那么这长方体原来的表面积是多少?

　　A.24

　　B.26

　　C.52

　　D.148

　　4. 已知一个三角形的三边长分别是5，17，X。若X为正整数，则这样的三角形有多少个?

　　A.3

　　B.6

　　C.9

　　D.12

　　5. 大圈半径是小圆半径的3倍，则大圆面积是小圆面积的：

　　A.3倍

　　B.6倍

　　C.9倍

　　D.3.14倍

　　翻页查看解析答案哦~

2022云南事业单位备考群
加群了解更多考试信息，获取更多备考资料

　　1.【答案】B

　　【解析】

　　第一步，本题考查几何问题，属于立体几何类。

　　第二步，如下图所示，搅棒斜放时，即与圆柱的对角线重合时上端露出杯口边缘最短，即圆柱对角线AC长为12-2=10(厘米);搅棒垂直放时，即与圆柱的高平行时上端露出杯口边缘最长，即圆柱的高AB为12-4=8(厘米)，根据勾股定理，可知BC=(厘米)，即圆柱底面直径为6厘米，故圆柱的容积为π×(6÷2)²×8=72π。
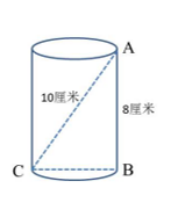因此，选择B选项。

　　2.【答案】D

　　【解析】

　　第一步，本题考查几何问题，属于立体几何类。

　　第二步，如图所示大坝的横断面如下：

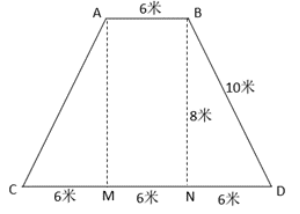　　等腰梯形ABCD中，MN=AB=6(米)，则DN=(18-6)÷2=6(米)。在△BND中，BN²=BD²-DN²=10²-6²=64，因此BN=8(米)。则梯形ABCD的面积=[(18+6)×8]÷2=96(平方米)。

　　第三步，大坝的体积为96×300=28800(立方米)，即混凝土需要28800立方米。

　　因此，选择D选项。

　　【拓展】

　　立体等腰梯形的体积=正截面(横断面)面积×总长度

　　3.【答案】C

　　【解析】

　　第一步，本题考查几何问题，属于立体几何类。

　　第二步，由于长方体的长、宽、高是连续的整数，则将它们长度分别设为x，x+1，x+2，又长方体各边长增加2之后，新长方体体积将增加4倍，则可列方程为5x(x+1)(x+2)=(x+2)(x+3)(x+4)，解得x=2，则该长方体原来的长、宽、高分别为2，3，4。

　　第三步，长方体原来的表面积为2×(2×3+2×4+3×4)=52。

　　因此，选择C选项。

　　4.【答案】C

　　【解析】

　　第一步，本题考查几何问题，属于几何特殊性质类。

　　第二步，在三角形中，根据两边之和大于第三边，得5+17>X;根据两边之差小于第三边，得17-5

　　第三步，因为X为正整数，所以可取13、14、15、16、17、18、19、20、21取1个值对应1个三角形，故能组成的三角形有9个。

　　因此，选择C选项。

　　5.【答案】C

　　【解析】

　　解法一：

　　第一步，本题考查几何问题，属于几何特殊性质类。

　　第二步，设小圆半径为x，则大圆半径为3x，根据圆面积的计算公式，圆的面积=πr²，则小圆面积为πx²，大圆面积为π(3x)²=9πx²，故大圆面积是小圆面积的9倍。

　　因此，选择C选项。

　　解法二：

　　第一步，本题考查几何问题，属于几何特殊性质类。

　　第二步，根据几何性质可知，当边长变为原来n倍式，则面积变为原来的n²倍，由大圆的半径是小圆半径的3倍，则大圆的面积是小圆面积的3²=9倍。

　　因此，选择C选项。